Una representación gráfica, al igual que una tabla o una ecuación, indica la relación que existe entre dos o más variables. Una representación gráfica también permite estimar valores si se tienen los puntos suficientes. Esto se puede realizar a través de la interpolación, donde se toman valores entre puntos, o a través de la extrapolación, que se obtiene al continuar los puntos.
Representación gráfica del calentamiento del agua. Este ejemplo dará una gráfica donde las variables x e y son directamente proporcionales.
Por ejemplo, al entregar energía térmica (calor) a un recipiente con agua, esta aumenta su temperatura. Entonces, existe una relación entre la energía entregada y la temperatura del agua. Cuando las magnitudes están relacionadas, se dice que una es función de la otra.
En el ejemplo señalado es fácil deducir que a mayor cantidad de energía entregada, mayor es la temperatura del agua. Sin embargo, lo importante es poder predecir lo más exactamente posible cuánto aumenta la temperatura cuando se le entrega una cantidad de energía determinada. A esto se pretende llegar cuando se busca la relación matemática que liga ambas variables, es decir, poder predecir el valor de una variable, para un valor conocido de la otra.
Esto es lo que vas a aprender
Representación gráfica de la relación directamente proporcional
Si al representar los valores de dos variables físicas en un gráfico se obtiene una recta que pasa por el origen, se dice que la relación entre ellas es directamente proporcional.
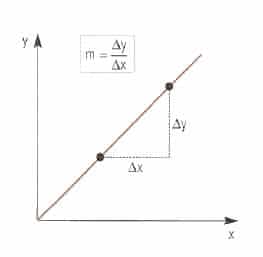
La pendiente m de la recta se calcula según:
![\[ \boxed{ m=\frac{\Delta_{y}}{\Delta_{x}}=\frac{{y_{2}-y_{1}}}{{x_{2}-x_{1}}}} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-37a16cb16f624ab9a86477faac563507_l3.png "Rendered by QuickLaTeX.com")
La unidad de medida que resulte al calcular la pendiente de una recta, corresponde a la unidad de medida de la variable física representada en el eje Y dividida por la unidad de medida de la variable física representada en el eje X.
Gráficos de relación lineal
Si al representar gráficamente los valores de dos variables se obtiene una recta que no pasa por el origen, se dice que ambas variables están relacionadas por una variación lineal o relación lineal.
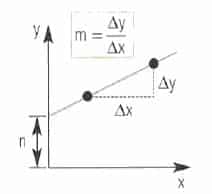
La relación matemática entre x e y es de la forma :
![\[ \boxed{ y=mx+n} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-8f13c3b0d2c0a26627d5a440e885cd0f_l3.png "Rendered by QuickLaTeX.com")
donde m está dada por la pendiente de la gráfica y n es el valor de y cuando x es igual a cero.
Gráficos de variación no lineal
Entre estos tipos de gráficos se tiene el de variación proporcional al cuadrado. En este caso, dos magnitudes, x e y, están relacionadas de modo que y es proporcional al cuadrado de x. Por ejemplo:
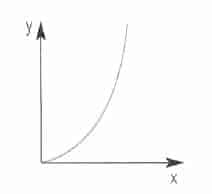
La representación gráfica de y en función de x es una curva denominada parábola.
![\[ \boxed{ y=mx^{2}} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-782123f5539a10445280f42b1f26673b_l3.png "Rendered by QuickLaTeX.com")
Gráficos de relaciones inversas
Entre estos tipos de gráficos se encuentra el de proporción inversa. En este caso, cuando x aumenta y disminuye proporcionalmente. Se dice entonces que y es inversamente proporcional a x. Por ejemplo:
La representación gráfica de y en función de x es una curva denominada hipérbola.
![\[ \boxed{ y=m\frac{1}{x}} \]](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-5092a9f58bfd4a7a8a638304ad21e227_l3.png "Rendered by QuickLaTeX.com")
