Home
Funciones trigonométricas

Funciones trigonométricas

Herramientas de la Física 0

La trigonometría se basa en las propiedades especiales del triángulo rectángulo. Por definición, un triángulo rectángulo es aquel que tiene un ángulo de 90°.

Si se considera el siguiente triángulo rectángulo:

Funciones trigonométricas

 

 

 

 

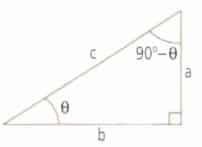
El lado a es el cateto opuesto al ángulo \theta;
El lado b es el cateto adyacente al ángulo \theta;
El lado e es la hipotenusa.

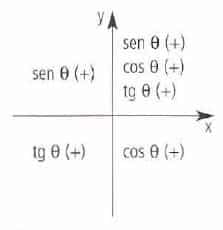
funciones-trigonometricas-signos

Funciones trigonométricas y sus signos. La figura muestra cuándo las funciones trigonométricas son positivas según el cuadrante donde se ubique el ángulo.

Las tres funciones trigonométricas básicas definidas por este triángulo son: seno (sen), coseno (cos) y tangente (tg). En función al ángulo \theta, estas funciones se definen del siguiente modo:

    \[ \boxed{ sen\; \theta=\frac{cateto\; opuesto\; a\; \theta}{hipotenusa}=\frac{a}{c}} \]

    \[ \boxed{ cos\; \theta=\frac{cateto\; adyacente\; a\; \theta}{hipotenusa}=\frac{b}{c}} \]

    \[ \boxed{ tg\; \theta=\frac{cateto\; opuesto\; a\; \theta}{cateto\; adyacente\; a\; \theta}=\frac{a}{b}} \]

Identidades pitagóricas

El teorema de Pitágoras proporciona la siguiente relación entre los lados de un triángulo rectángulo:

    \[ \boxed{ c^{2}=a^{2}+b^{2}} \]

a partir de este teorema y las definiciones de las funciones trigonométricas básicas, se tiene que:

    \[ \boxed{ cos^{2}\; \theta\; +\;sen^{2}\; \theta=1} \]

    \[ \boxed{ tg\;\theta =\frac{sen\;\theta }{cos\;\theta }} \]

Ley del seno y coseno

Las relaciones que se muestran a continuación, se aplican a cualquier tipo de triángulo. Por ejemplo,

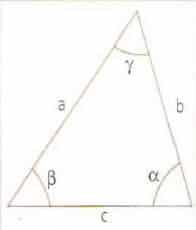
ley-seno-coseno

\alpha +\beta +\gamma =180^{\circ}

Ley del coseno

    \[ \boxed{ a^{2}=b^{2}+c^{2}-2bc \; cos\; \alpha } \]

    \[ \boxed{ b^{2}=a^{2}+c^{2}-2ac \; cos\; \beta } \]

    \[ \boxed{ c^{2}=a^{2}+b^{2}-2ab \; cos\; \gamma } \]

Ley del seno

    \[ \boxed{ \frac{a}{sen\; \alpha }=\frac{b}{sen\; \beta }=\frac{c}{sen\; \gamma }} \]

Related