A la cantidad de dígitos conocidos con certeza en una medida se le denomina número de cifras significativas (cs). Por ejemplo, la medida 430,23 gramos tiene cinco cifras significativas, y la medida 0,032 gramos tiene solo dos cifras significativas.
El número de cifras significativas no es siempre claro. Por ejemplo, si la distancia entre dos puntos es exactamente
20 [cm], con una incerteza de 1 ó 2 [cm], entonces, el 20 tiene dos cifras significativas; si la incerteza es de ± 0,1 [cm], se escribe 20,0 [cm]. Pero para valores aproximados, si la distancia es aproximadamente 10 [cm], solo existe una cifra significativa, el 1, ya que el cero es un retenedor de espacio (puede ser, por ejemplo, 9, 11 ó 12).
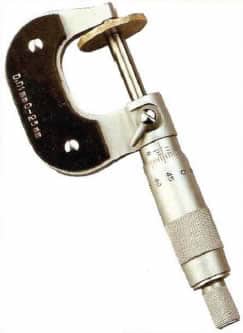
Tornillo micrométrico.Instrumento usado para medir longitudes en mm hasta la milésima.
Reglas para determinar cifras significativas
- Todo número distinto de 0 es significativo.
Por ejemplo: 473 g tiene 3 cs. - Los ceros entre los números son significativos.
Por ejemplo: 31,084 cm tiene 5 cs. - Los ceros que están a la derecha del número son significativos.
Por ejemplo: 0,0750 g tiene 3 cs. - Los ceros en la izquierda de los números no son significativos.
Por ejemplo: 0,0024 mm tiene 2 cs. - Si los ceros están después de los números, para un valor entero, pueden ser o no cifras significativas. En este caso se recomienda la notación científica.
Por ejemplo, 8.000 se expresa como 8 x 103. - Al sumar o restar, el número de posiciones decimales del resultado debe ser igual al número menor de posiciones decimales de cualquier término de la suma o resta.
Por ejemplo: al sumar 2,345 + 0, 11 . En este caso, serían 2 cifras decimales, ya que 0, 11 tiene el valor más bajo de cifras decimales. Entonces, el resultado será: 2,345 + 0, 11 = 2,455 = 2,46. - Al multiplicar o dividir, el resultado final debe tener tantos dígitos como la medida con el menor número de cifras significativas utilizado en el cálculo.
Por ejemplo: 2,25 x 2,1 = 4, 725 = 4, 7
Redondeando un número
Cuando el resultado de un cálculo posee una mayor cantidad de números del que permite la regla, se debe aproximar o redondear este resultado. El criterio que se utiliza es el siguiente:
- Si el número es mayor o igual a cinco, se aumenta en una unidad el número anterior. Ej.:
1,29 = 1,3
6,458 = 6,46 - Si el número es menor que cinco, no se aumenta y se eliminan las cifras restantes. Ej.:
1,24 =1,2
9,342 = 9,34