Home
Movimiento circular uniforme

Movimiento circular uniforme

Cinemática 0

El movimiento circular uniforme (MCU) corresponde al movimiento de los cuerpos que describen una circunferencia con rapidez constante y velocidad variable. En el caso de la velocidad, el valor no cambia pero sí su dirección. En un movimiento circular uniforme:

  • El tiempo que se demora el cuerpo en dar cada vuelta es siempre el mismo, es decir, el movimiento es periódico. Por lo tanto, la rapidez se puede calcular como la distancia/tiempo, en la forma:Movimiento circular uniforme

        \[ \boxed{ v=\frac{2\; \pi \; r}{T}} \]

    donde:

    r es el radio de la circunferencia
    t es el período.

  • El vector velocidad cambia de dirección en cada punto de la trayectoria circular, lo que origina una aceleración. El valor de la aceleración llamada centrípeta es:

        \[ \boxed{ a_{c}=\frac{v^{2}}{r}} \]

    donde:

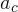    a_{c} es un vector que se dirige hacia el centro de la circunferencia.

Aceleración centrípeta en el movimiento circular uniforme

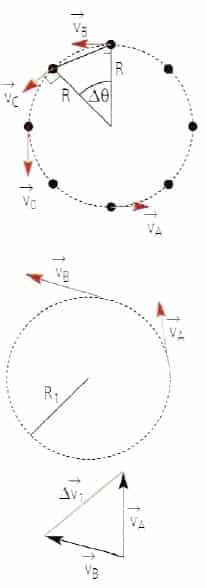
Al tomar dos puntos A y B de una circunferencia y trasladar el vector v_{B} paralelamente hasta que su origen coincida con el punto A, se obtendrán dos triángulos semejantes; el primero formado por los radios, y el segundo, por las magnitudes de las velocidades. Luego, los lados de dichos triángulos son proporcionales. Entonces se cumple que:

    \[ \frac{\Delta r}{r}=\frac{\Delta v}{v}\; \; \; \; \; \; \;\; \; \; \; v\; \; \Delta r= r\; \Delta v \]

Dividiendo por el tiempo, esta última expresión resulta ser:

    \[ \boxed{ v\frac{\Delta r}{\Delta t}=r\frac{\Delta v}{\Delta t}} \]

Aceleración centrípeta

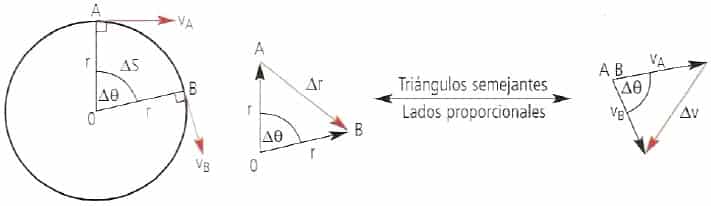
Aplicando las definiciones pertinentes, finalmente se obtrene una expresión para la aceleración, cuya dirección es radial y su sentrdo está dirigido hacia el centro de la circunferencia, por lo que corresponde a la aceleración centrípeta:

    \[ \boxed{ a_{c}=\frac{v^{2}}{r}} \]

Medidas angulares

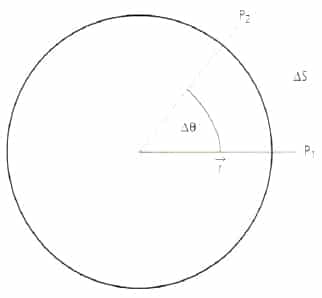
Vectorialmente, un movimiento circular uniforme se puede describir a través de medidas angulares, es decir, en relación al ángulo que se describe. Por ejemplo, cuando un objeto se desplaza en una trayectoria circular entre los puntos P_{1} y P_{2}, el radio r describe un arco de circunferencia \Delta S, barriendo un ángulo \Delta \theta, tal que:

Medidas angulares

    \[ \Delta \theta =\frac{\Delta S}{r} \]

Cuando el valor del arco descrito es igual al radio de la circunferencia el ángulo del centro mide 1 radián. En términos simples:

    \[ \theta =\frac{S}{r} \]

por ejemplo,

    \begin{align*} 360^{\circ} &= \frac{2\; \pi\; r}{r}\\ 360^{\circ} &= 2\; \pi \; rad\\ 180^{\circ} &= \pi \; rad\\ 90^{\circ} &= \frac{\pi }{2}\; rad\\ 57,2958^{\circ} &= 1 \; rad \end{align*}

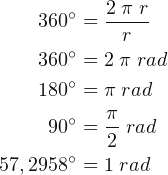
Velocidad angular

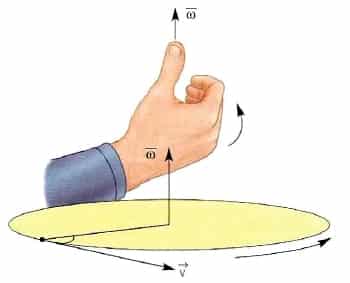
La velocidad angular media (\bar{\omega}) es la variación del ángulo del centro barrido durante un intervalo de tiempo, su dirección es perpendicular al plano que cont iene la circunferencia y su sentido se rige por la regla de la mano derecha.

Sea \Delta \theta la variación del ángulo barrido en el intervalo \Delta t, entonces, la velocidad angular media \bar{\omega}_{m} está dada por:

    \[ \boxed{ \bar{\omega}_{m}=\frac{\Delta \theta }{\Delta t}\; \; \; \;\; \; \begin{bmatrix} \frac{rad}{s} \end{bmatrix}} \]

Velocidad angular

Aceleración angular

Suponiendo que una partícula se mueve en una trayectoria circular cuya velocidad angular \omega [rad/s] varía a través del tiempo, entonces, se define operacionalmente la aceleración angular (\bar{\alpha }) como el cociente entre la variación de la velocidad angular y el intervalo de tiempo:

    \[ \boxed{ \bar{\alpha }=\frac{\Delta \bar{\omega} }{\Delta t}} \]

Por lo tanto, el movimiento circunferencial uniforme se caracteriza por
tener:

    \[ \bar{\omega}=cte \; \; \; \; y \; \; \; \;\alpha =0 \]

La aceleración angular \bar{\alpha } se mide en rad/s^{2}.

Relación entre medidas lineales y angulares

La relación que se establece entre las medidas lineales y angulares es:

    \[ \Delta S=r\; \; \Delta \theta \]

Como esta relación se produce en un pequeño intervalo de tiempo, se divide por ót, quedando:

    \[ \frac{\Delta S}{\Delta t}=\frac{r\; \Delta \theta }{\Delta t} \]

así, de acuerdo a estas expresiones, se puede determinar que:

  • la rapidez lineal será:

        \[ \boxed{ x=r\; \omega } \]

  • la aceleración lineal o tangencial:

        \[ \boxed{ a_{T}=r\; a} \]

  • la aceleración centrípeta:

        \[ \boxed{ a_{c}=\frac{v^{2}}{r}} \]

        \[ \boxed{ a_{c}=r\; \omega^{2} } \]

Ejercicio resuelto

1. Un carrusel en rotación da una revolución en 4 [s]. ¿Cuál es la rapidez lineal de un niño sentado a 1,20 [m] del centro?

La frecuencia angular del carrusel es 1/4 [rev/s]. Como una revolución es una vuelta completa que corresponde a 2\pi radianes, la velocidad angular del carrusel es:

    \[ \omega =2\pi f=2\pi \; \; rad/\not{rev} \times 1/4\; \; \not{rev}/s \; \; \; \; \; \omega =1,57\; \left [ rad/s\right ] \]

La rapidez lineal del niño es, por lo tanto:

    \[ v=r\; \omega =1,20\; m\; \times \; 1,57 \; rad/s\; \; \; \; \; \; v=1,88\left [m/s \right ] \]

Related