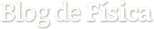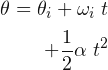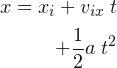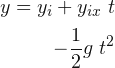El movimiento circular uniformemente variado (MCUV) corresponde al movimiento cuya trayectoria es curva y la velocidad es variable. Este movimiento, además de presentar aceleración centrípeta, como el caso del movimiento circular uniforme, presenta aceleración tangencial y aceleración angular. La aceleración tangencial aparece por efecto de la variación de la magnitud de la velocidad y la aceleración angular, por efecto de la variación de la velocidad angular.
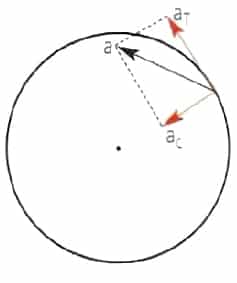
Cuando existen las dos aceleraciones, tangencial y centrípeta, la aceleración resultante es:
![]()
Las relaciones angulares indican el comportamiento de un cuerpo en un movimiento circular uniformemente variado, por ello deben ser estructuralmente invariantes frente a otros sistemas de referencias; en una dimensión o en dos dimensiones. Esto se resume en el siguiente cuadro:
| Relaciones | Angulares | Horizontales | Verticales |
|---|---|---|---|
| Posición | |||
| Velocidad | |||
| Aceleración | |||
| Ecuación de movimiento | |||
| Ecuación de itinerario |
|
|
|
| Ecuación de velocidad-desplazamiento |
Una relación simple para enlazar los conceptos del movimiento tangencial y angular es:
![]()
donde:
![]() es el radio de la circunferencia .
es el radio de la circunferencia .
![]() es el arco barrido .
es el arco barrido .
![]() es el ángulo del centro (en radianes).
es el ángulo del centro (en radianes).
![]() es la rapidez tangencial o lineal.
es la rapidez tangencial o lineal.
![]() es la rapidez angular.
es la rapidez angular.
![]() es la aceleración tangencial.
es la aceleración tangencial.
![]() es la aceleración angular.
es la aceleración angular.
Ejercicio resuelto
1. Un auto que tiene sus ruedas de 0,8 [m] de diámetro, avanza a 108 [km/h] (30 m/s). Si el auto drásticamente frena y sus ruedas, uniformemente, dan 30 [vueltas] completas, determinar: a. la velocidad angular inicial. b. el desplazamiento angular. c. la aceleración angular. d. el desplazamiento del auto.
a. La velocidad angular inicial está dada por:
![Rendered by QuickLaTeX.com \begin{align*} & \omega_{i} =\frac{v}{r}=\frac{30\; m/s}{0,4\; m}\\ & \omega_{i} =75\; \left [ rad/s \right ] \end{align*}](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-54c7b3f8f432688d101769b98cf8ae49_l3.png)
b. El desplazamiento angular corresponde al número de vueltas en radianes, es decir:
![Rendered by QuickLaTeX.com \begin{align*} & \Delta \theta = 2\pi \left [ N^{\circ}de\; vueltas \right ]\\ & \Delta \theta = 30\times 2\; \pi \\ & \Delta \theta = 60\pi \left [ rad \right ] \end{align*}](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-430f398fc970bf9f4c419b5e2892cdba_l3.png)
c. Para calcular la aceleración angular, al detenerse, la velocidad angular final es nula; además, como no se conoce el tiempo, se recurre a la relación velocidad-desplazamiento:
![Rendered by QuickLaTeX.com \begin{align*} & \omega ^{2} = \omega_{i}^{2}+2\alpha \; \Delta \theta \\ & 0^{2} = 75^{2}+2\alpha\; \; 60\pi \; \; \; \; \; \; \; \; \left [ \pi =3,14 \right ] \\ & \alpha = 14,9\left [ rad/s^{2} \right ] \end{align*}](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-b27d7c75bc017050f3aa2b6010254d98_l3.png)
d. El desplazamiento del auto se determina sabiendo que
![Rendered by QuickLaTeX.com \begin{align*} & \Delta x = \Delta S=\Delta \; \theta \; r \; \; \; \; \; \;\; \;\;\; luego\\ & \Delta x = 60\pi \times 0,4\left [ m \right ] \\ & \Delta x = 75,36\left [ m \right ] \end{align*}](https://www.blogdefisica.com/wp-content/ql-cache/quicklatex.com-fa22a6d1476634fb4f1e06c531f1cf3e_l3.png)