Energía potencial elástica » Blog de Física

La energía potencial elástica es la energía asociada con los materiales elásticos. Por ejemplo, un resorte al ser comprimido o elongado almacena energía potencial elástica y, al ser soltado, puede realizar trabajo sobre un objeto.

Para mantener el resorte comprimido o alargado una cierta longitud $x$ , a partir de su largo natural, es necesario que, en este caso, la mano aplique una fuerza $F_{M}$ sobre el resorte; esta fuerza es directamente proporcional a $x$ .

Energía potencial elástica. Al estirar o comprimir un resorte se almacena energía potencial elástica en él.

$\boxed{ F_{M}=kx}$

$k$ es una constante conocida como constante de rigidez del resorte.

El resorte, a su vez, ejerce una fuerza $F_{R}$ para regresar a su longitud natural, fuerza que recibe el nombre de fuerza restauradora, porque está ejercida en dirección opuesta al desplazamiento $x$ .

$\boxed{ F_{R}= - kx }$

Ecuación conocida como ley de Hooke.

Para encontrar una expresión que describa la energía potencial asociada con la fuerza del resorte, se determina el trabajo que se requiere para comprimir el resorte desde su posición de equilibrio hasta cierta posición final arbitraria $x$ . Debido a que la fuerza varía desde $O$ hasta $kx$ , se utiliza la fuerza promedio $\frac{(F_{0}+F_{X})}{2}$ .

$\bar{F}=\frac{0+K X}{2}=\frac{1}{2}kx$

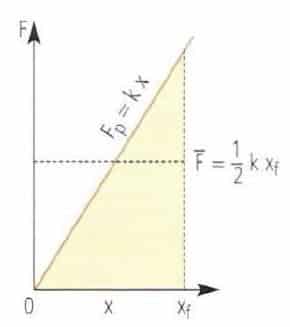
Fuerza sobre un resorte. La fuerza para estirar un resorte aumenta linealmente con su elongación .

El trabajo realizado por la fuerza aplicada será: $W=\bar{Fx}=\frac{1}{2}kx^{2}$

El trabajo realizado se almacena en el resorte comprimido en forma de energía potencial elástica como:

$\boxed{ Ep_{elas}=\frac{1}{2}kx^{2}}$

Una vez que se ha comprimido o estirado el resorte respecto a su posición de equilibrio, la energía potencial elástica se puede considerar como la energía almacenada en el resorte deformado. Esta energía siempre es positiva en un objeto deformado al depender de $x^{2}$ .

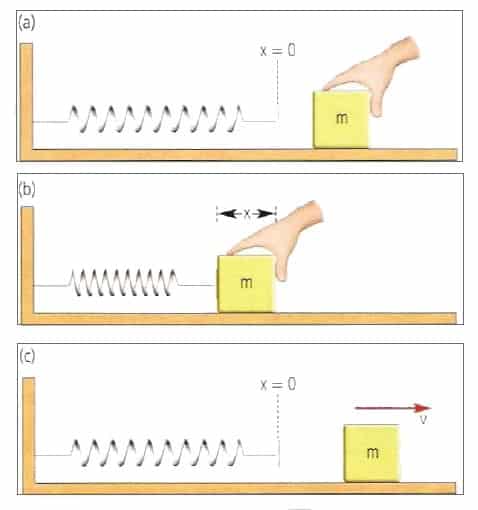
Por ejemplo, en la figura se observa que un resorte realiza trabajo sobre un bloque. El resorte que se encuentra sin deformar (a) cuando es empujado por un bloque de masa $m$ , se comprime una distancia $x$ (b). Cuando el bloque se suelta (c), partiendo del reposo, la energía potencial plástica almacenada en el sistema se transforma en energía cinética del bloque.

Energía potencial elástica: ejercicio resuelto

1. En una prueba experimental de alcance, un dardo de goma de $80,0 [g]$ es presionado contra un resorte. El resorte, de constante $k= 250 [N/m]$ , se comprime $5,00 [cm]$ y se libera. Si el dardo abandona el resorte cuando este alcanza su longitud natural, ¿qué rapidez adquiere el dardo? (Despreciar la fricción).

Cuando el resorte es comprimido por el dardo, la energía potencial que almacena será:

$Ep_{elas}=\frac{1}{2}kx^{2}=\frac{1}{2}(250N/m)(-5\cdot 10^{2} m)^{2}$

$Ep_{elas}=0,313 [J]$

Cuando el dardo se libera partiendo del reposo, la energía potencial elástica almacenada en el sistema se transforma en energía cinética $(\frac{1}{2}mv^{2})$ del dardo, por lo que, al despejar, la rapidez queda:

$V=\sqrt{\frac{2E_{k}}{m}}=\sqrt{\frac{2(0,313J)}{80\cdot 10^{-3} kg}}$

$\boxed{ V=2,80[m/s] }$

Energía potencial elástica: ejercicio resuelto

Related