Home
Movimiento relativo

Movimiento relativo

Cinemática 0

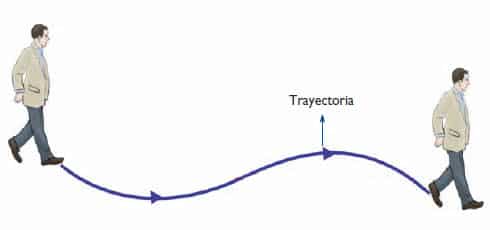
Observadores en diferentes marcos de referencia pueden medir distintos desplazamientos o velocidades de un cuerpo en movimiento. Cuando dos observadores que se desplazan uno respecto al otro no realizan observaciones, ni mediciones coincidentes respecto a un mismo suceso, se dice que es un movimiento relativo al observador.

Por ejemplo, si se tiene un bote que se mueve con velocidad \vec{V}_{BA} respecto al agua de un río, se observará lo siguiente:

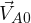  • movimiento-relativo-1Si el agua del río está en reposo, es decir, la velocidad del agua respecto a la orilla (\vec{V}_{A0}) es cero, un observador que se encuentre en la orilla del río verá que la velocidad del bote respecto al agua (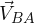\vec{V}_{BA}) y respecto a la orilla (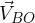\vec{V}_{BO}) es la misma. De acuerdo al observador de la orilla, se cumple: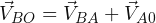\vec{V}_{BO}=\vec{V}_{BA}+\vec{V}_{A0}\; \; \;, como 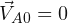\vec{V}_{A0}= 0, entonces:

        \[ \boxed{ \vec{V}_{BO}=\vec{V}_{BA}} \]

  • Movimiento relativo

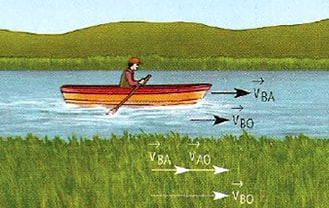
    Debido a la corriente del río la embarcación tiene una velocidad respecto al agua que es diferente a la velocidad que tiene respecto a la orilla (Tierra), es por esto que se habla de velocidad o movimiento relativo.

    Si el agua se mueve con cierta velocidad (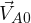\vec{V}_{A0}) respecto a la orilla, y el bote se mueve con una velocidad (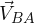\vec{V}_{BA}) respecto al agua y en el mismo sentido que esta, un observador que se encuentre en la orilla del río verá que la velocidad del bote (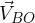\vec{V}_{BO}) respecto a la orilla es mayor, debido a que se suma la velocidad del bote con la velocidad de arrastre del agua del río. Esta situación se expresa según:

        \[ \boxed{ \vec{V}_{BO}=\vec{V}_{BA}+\vec{V}_{A0}} \]

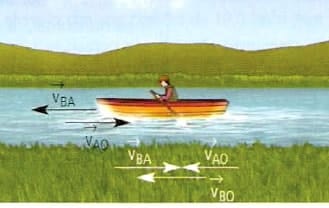
  • movimiento-relativo-3
    Sin embargo, si el bote se dirige en sentido contrario al agua, es decir, río arriba, el observador verá que la velocidad del bote es menor, ya que se resta la velocidad del bote con la velocidad de arrastre del agua. Esta situación se expresa según:

        \[ \boxed{ \vec{V}_{BO}=-\vec{V}_{BA}+\vec{V}_{A0}} \]

Ejercicio resuelto

1. Los instrumentos de un avión indican que vuela hacia el este a 325 [km/h] y desde la torre se le indica que un viento sopla en ese instante hacia el norte a 64 [km/h]. ¿Cuál es la velocidad del avión respecto a la torre de comandos?

Datos:

– Sistema de referencia 1: velocidad del avión respecto al aire \vec{V}_{Aa}
– Sistema de referencia 2: velocidad del avión respecto a la Tierra \vec{V}_{AT}
velocidad del aire respecto de Tierra \vec{V}_{aT}

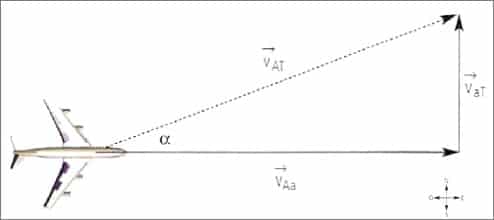
movimiento-relativo-ejemplo

La ecuación vectorial de velocidad del avión con respecto de la Tierra es:

    \[ \vec{V}_{AT}=\vec{V}_{Aa}+\vec{V}_{aT} \]

Luego, según los módulos de los vectores:

    \begin{align*} {V}_{AT} &= \sqrt{V_{Aa}^{2}+V_{aT}^{2}}\\ {V}_{AT} &= \sqrt{(325\; km/h)^{2}+(64\; km/h)^{2}}\\ {V}_{AT} &= 331,2\; [km/h] \end{align*}

El ángulo será de:

    \[ \alpha =arctg\; \frac{64}{325}\; \; \; \; \;\; \;\; \; \alpha =11,1^{^{\circ}} \]

Related